Everything Else I Know About Music
As the first post in this series has been received pretty well, at least by those who managed to finish the 5000-word monster, here's the sequel. Everything else I know about music theory.
The first part seemed to resonate the most with the people already proficient with their instruments, but who never bothered to delve too deeply into music theory. In this post, we'll continue in the same vein, elaborating on some simplifications from the first part, while also covering some new ground.
Chords, Advanced
One of the biggest lies implied from the first part was saying that chords always consist of three notes. Even though it is true that the majority of the chords you encounter will be three-noters, in theory you can do a bit more.
The chords we've shown, both major or minor ones, are constructed by stacking intervals - we start with the first note, add its third, and then its fifth. But we can continue with this. If you add a seventh interval to it, you'd get something that we call, simple enough, a seventh chord.
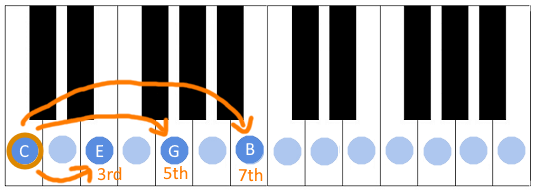
The seventh chords are harmonically more complex than the third ones. More notes at the same time means they clash with each other a bit more, so you get a sound that is not as "clean", which is why you won't hear them as much in regular pop music. But in more complex genres like funk or jazz, they're pretty common.
As we've learned, three-note chords come in two types, depending on which third interval, a major or minor one, we use to construct them. For seventh chords this gets more complicated. As we can add a major or minor seventh to either a major or minor chord, we get four combinations here, and each of them has its own confusing name. Let's see:
Personally, I can never seem to remember the difference, so on a guitar I always have to look up the exact finger shape to use to play them. Luckily, if you're learning a guitar song, you can often assume that the original author meant to use the chord that's easiest to play, so it all kind of works out in the end.
Proceeding in the same manner, we have five-note chords which we call pentachords, and the most common one would be a ninth chord:
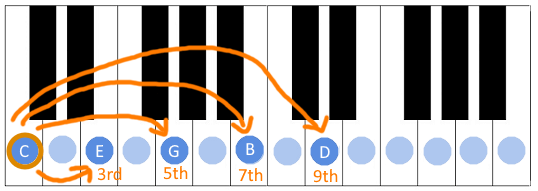
To a practically-minded musician, this is simple enough - you just stick an additional ninth interval in there.
Just like with sevenths, when you add more notes, the sound gets a bit more complex. You can't really say the chord is "happy" or "sad" anymore, like you could for three-note chords. You can see that added ninth is basically a second interval to our root note, which means that in the same chord we have both a first and second, the adjacent notes, which will always clash with each other when together. Although, that effect is not as pronounced when they're an octave apart, which is why we're calling it ninth and not a second interval, even though they're the same note.
Stacking intervals is very logical and math-ey, but some things are convention driven instead. For example, we said that the ninth chord contains the seventh interval. But since we can also have a sixth chord (major/minor triad with added sixth interval), does that mean our seventh chord should also contain the notes from the sixth chord, just like ninth contains sevenths? The answer is no. I couldn't find a logical explanation for this, so it seems to just be a convention based on what sounded good. So sixth chords are always four-noters, just like the seventh chords are. But all subsequent combinations keep increasing the note count - ninth chords are five-noters, eleventh chords six-noters, and thirteen chords seven-noters, somehow using all notes from the scale.
If you don't want this stacking bonanza, and you'd rather like to have a ninth chord that doesn't contain a seventh interval, there's a separate notation for that - add9. So a Cadd9 chord would be a C with added 9th interval. And you can use this notation for other intervals as well, freely as you'd want.
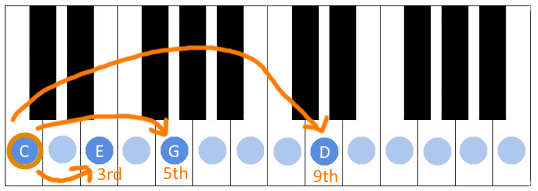
But the point is - you don't have to look at chords as some unchangeable combinations of notes that you learn by heart. They are just convention-based shorthands for various interval combinations that sound good together. You can always spice them up by adding or removing some notes from the mix, without even asking yourself "what chord is this"?
To cap this section, let's try to see which chord is played when you strum all open strings on a guitar. Is it even a chord? I never considered it as such as it didn't match any of the chords I learned, but as chords are just combinations of intervals, it really is one. Let's see.
The lowest note in a chord is usually a root note, and in this case it's E, so this has to be some variation of an E chord. The second string is A, which to our root note is a fourth interval, not something that's common in major/minor chords, so it's gonna be something with add4. The third string is D, which we can recognize as the minor seventh interval (10 steps apart), so it must be some minor seventh chord. The last three notes G, B and E, are third, fifth and an octave of our base note E, which you can recognize to be a regular three-note chord shape. But the third here is a minor one (three semitones apart), so it must be a minor chord. So what we have is an E minor chord with added fourth and seventh intervals - meaning it's E minor seventh with added fourth - Em7add4.
You could also reach the same conclusion by playing the most similar chord shape to the open strings, Em7, played with only one finger, and then see which interval you get when you remove that one finger. It's fourth, so again we get Em7add4.
Chords Under Distortion
On a guitar, riffs are often played using so-called fifth or power chords, which consist of only two notes: a root and its fifth. Music theory purists might argue that they're not real chords due to their indeterminate nature, e.g. they're neither a major nor a minor chord. And if you try playing them on a piano, they do sound like they're missing something.
However, when you apply a distortion effect on a guitar, as is common in rock music, funny things happen. Due to some underlying "physics of sound" things, additional harmonic content gets generated and they do start to sound like full chords.
This is because each note actually contains parts of other notes, called harmonics. They are barely audible in normal conditions, but with distortion - which basically increases the volume of a sound above its allowed maximum levels, cutting the main waveform off - suddenly harmonics become louder relative to the main note you just played.
In other words, distortion surfaces few additional notes out of the note you just played, which creates additional harmonic content, so the plain two-note power chords do get to sound fuller, like "proper" chords.
For an example, I loaded up FL Studio, played a single note on a regular sine-wave synth and analyzed the result with a spectrogram. You can see only a single note is there:
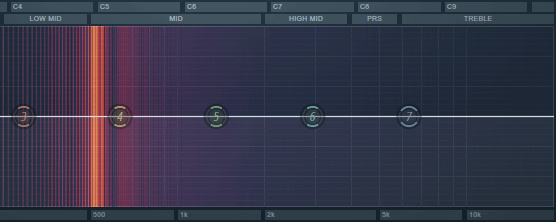
However, when you apply distortion to it (or use a square wave, which is basically the same thing) it starts to looks like this, with a bunch of new notes appearing out of thin air:
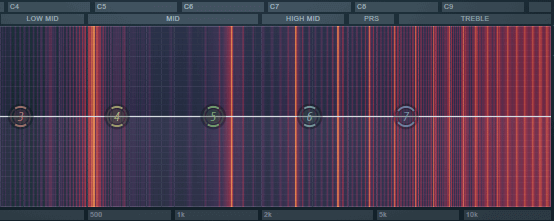
These extra "notes" will make the harmonically neutral two-note "chords" sound like full ones. And it's the same reason why regular three-or-more-note chords under distortion sound bad - the additional harmonic content will make them too dissonant, as if you're playing something more complex, like 11th or 13th chords.
If you want to know why this happens, it's called the harmonic series and without going too much in-depth, here's a great video about it.
Scales and Modes
In the previous post, we've shown that major and minor scale can use the same notes but still sound different, as they're constructed using different formulas. So with white keys only, if you start playing your scale on a C, it's gonna be a major scale, and if you start it on an A, it will be a minor.
But what if you start it on some other note in the scale? You can do that, and in that case you'd be playing one of the modes. They are like scales, but due to different formulas they sound a bit different.
There are seven modes, one for each note, and they have some exotic names hailing from the ancient Greek regions where they originated from - Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian and Locrian.
So for example, using white notes only, if you played a scale that started and ended on a note D, you'd be playing in D Dorian mode. If you started on E, that'd be E Phrygian. They all use the same notes, but arranged with a different formula, which results in different moods.
Now, why exactly modes are a separate concept from scales eludes me (in fact, Ionian mode is the same thing as a major scale, and Aeolian as minor), but they're useful to know to understand that, just like with chords, there's nothing special in the formulas we use for them, and that other combinations can exist.
Modes can be found in contemporary music sometimes. For example, Dorian mode is often called "funk minor scale" and can be heard in Get Lucky or Crosseyed and Painless, but you can also make it sound medieval, like it's done in Scarborough Fair. Locrian might be the least common, as it doesn't have a proper fifth interval, so you can't construct many of the usual chords you're used to. But Björk did it anyway.
But back to the scales. The point is that the formulas we use aren't set in stone and you can modify them if you know what you're doing. For example, one cool variation of a minor scale is the harmonic minor scale, which you can get by raising its seventh step by one semitone. Just changing one interval is enough to alter it to get that exotic Middle-eastern sound.
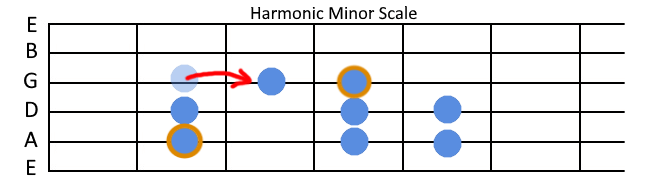
But it's not the only scale with that feel - Phrygian mode can sound similar, as shown in the example of The Offspring - Come Out And Play, and there's also the Arabian scale, which is just a Major Locrian scale (modified Locrian mode with two notes sharpened). But it doesn't even matter what they're called, as their feel is not coming from their names, but from the intervals they're made of. And which of those intervals you're accenting.
Just like chords, scales are stacks of intervals and you're allowed to construct them from whatever intervals you want. Here's a video of Josh Homme from QOTSA showing a scale he found out when he was a kid and has been playing it for 20 years without even knowing what's it called. And that is okay.
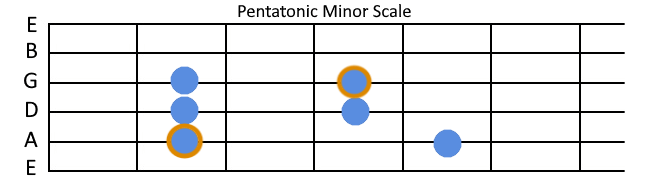
And then of course, you can remove some of the notes from the scale. One example of such minimal scales are the pentatonic minor and major scales. Penta meaning five, which means we remove two notes. This is useful because fewer notes means less chance of them clashing with each other, which makes soloing in them really easy. Playing anything in them will sound good over the progression in the same key.
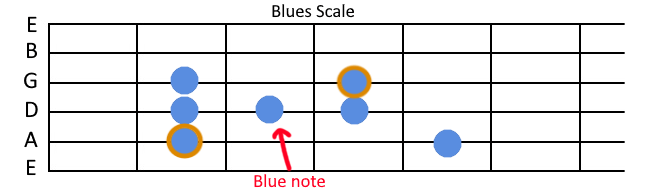
Another popular variation of this is the 6-note "blues scale", which adds the so-called "blue note" to the pentatonic scale, which produces recognizable sound found in blues music. Fun fact about the blue note is that it's traditionally played a bit "out of pitch", bent just a tiny bit above where the note should be. This might seem like it's wrong, but considering modern music uses just-intonation format where all the notes are a bit off from what they naturally should be, by bending it, blues players actually hit the most correct version of the note. This means that on instruments that can't bend, like pianos, you can't hit a "proper" blue note.
Time Signatures
This is also one of the things which looks awfully complex at first, but is dead simple when you realize how much of it is, again, driven by convention. So let's see.
A time signature is written as a fractional number like this: 4/4, with the first number telling you how much of something there is, and the second of what it is. In the example of 4/4, it means that we have four quarter notes. In another example of 6/8, it means that we have six eight notes. But don't worry - you don't need to know about note lengths here, half, quarters, eight notes or whatnot.
For all practical purposes you only need to know this: in quarter notes, all of them are accented beats, in eight notes only some of them are. Let's see the examples.
The 4/4 is the most common time signature, usually just called "common time" due to how commonly common it is. The bulk majority of music you heard in your life is written in this, and you already know how to recognize it. Turn on the radio, and start tapping your foot to the rhythm. Each tap here is a quarter note, and you will notice it's always packed in groups of four taps per measure.
It's the regular kick-snare rhythm found in pop/rock music, or a four-on-the-floor in electronic, it's all 4/4.
Likewise, if a song makes you tap in groups of threes, that would be a 3/4. That signature is not as common in western music, but you can find it in other places, for example waltz dance. So far so good.
Eight note time signatures are different, as in them not all of the notes are accented. Let's take 6/8, the most common of the bunch. It means notes are grouped in packs of sixes, and their lengths are eight notes. And we don't accent all the notes, otherwise that would be just 6/4. So how do we count it, how do we know which of the six are accented?
This is where the conventions come in - it's not a rule or anything, but most of the songs in 6/8 will have the stress on the first and fourth beat, so we'll count them as "ONE two three FOUR five six". So we'll be counting to six, but only stressing (tapping the foot) on beats one and four. For an example, take Elvis Presley - Can't Help Falling In Love.
Of course, for your music you get to choose where to put the accents, but the majority of 6/8 music in the wild will have it on one and four.
So, what would a 8/8 time signature look like? Those are eight notes, so we're not supposed to stress all 8 of them (otherwise it would be a 8/4 signature). And we can pick where to put the stress. If we decide to stress every second one, we'd get "ONE two THREE four FIVE six SEVEN eight". Which as you can see, even though it's counted differently, still produces the same rhythm that we had in our 4/4 example! So is 8/8 same as 4/4? This brings us to one misconception about this: time signatures are not rhythms.
Time signature is just a format that the author chose to write the song in a music sheet, because it was the easiest one to count it with. So if a song is in 6/8, it means "if you were to write this song in a music sheet, the most convenient way to lay out the notes on the paper would be to use the 6/8 time signature". And the easiest way to play it would be by counting it that way. But no one is preventing you from writing the same rhythm in 3/4, or maybe even 4/4, however unreadable that music sheet might end up.
So a 4/4 and 8/8 are the same time signatures? Nope, but they can be the same rhythm, depending on where you put the accents on.
One common 8/8 rhythm is when you count it in groups of 3+3+2, like "ONE two three FOUR five six SEVEN eight", like in Coldplay - Clocks. But I've often seen that rhythm referred to as 4/4, even though you don't really have four accented quarter notes there. But time signatures are not about rhythms, they're about the music sheet format in which you'll write your rhythm in. And you can easily do a 3+3+2 rhythm inside of a 4/4 grid, so there's no need to complicate by calling it 8/8.
Knowing all of this might be an overkill for a practical everyday musician, though, so we can condense it into few simpler shorthands.
For quarter note rhythms, you accent every beat. Conventionally, you do it in groups of fours, but you can use the other numbers as well, like Pink Floyd - Money which is in 7/4. If you try to play in fives or sevenths, you'll notice just how much 4/4 is ingrained in our feel for music and how unnatural it is to play anything else.
For eight note rhythms, you accent only some of the beats. As said, 6/8 is the most common one, but you can sometimes find 12/8 which is counted in four groups of threes, like in Tame Impala - Lost In Yesterday. This one could also be considered as a 4/4 with triplets, or maybe even as a 6/8, but it doesn't matter, because it's just a time signature.
Eight note combinations can produce some irregular ryhthms that will throw you off at first, because they'll either be missing half a beat, or have one extra. You can find exotic examples of this in King Gizzard & The Lizard Wizard in 5/8, Cat Stevens in 7/8 and Golden Brown which is 13/8 during the intro. Also, two famous examples of a 5/4 rhythm are Mission Impossible theme and Dave Brubeck's Take Five, both of which I personally find easier to count in 10/8 (3 + 3 + 2 + 2) instead. Honorary mention goes to Tool, who are too insane to be covered in this post.
Breaking the rhythm down into groups of 2's and 3's makes those more complex time signatures a bit less scary, as you're just counting to twos or threes. In fact, as 7/8 is somewhat common in the traditional music of the Balkans, a lot of compositions start not with the classic 4/4 drumstick lead-in, but rather by a singer counting off to seven like "ONE two three ONE two ONE two", like in Dado Topić - Makedonija.
Playing those off-kilter rhythms is a bit weird at first, but it's a good practice. I'd suggest everyone to try it, at least so you can see just how 4/4 has become an automatic thing for most of us raised on western music. Speaking of which...
The Universality of Music in Time and Place
Is music global? Is music universal? Was the music invented, or was it discovered?
Today's music framework is built around certain physical characteristics of sound, which are the same everywhere in the known universe. Each sound wave vibrates at a certain frequency, expressed in hertz (Hz). If you play some sound wave along with another sound wave vibrating at double its frequency, they will sound good together - almost like they're the same sound. Such a pair of sound waves, with frequency ratios of 2:1, we decided to call "an octave" and use as the base for our music theory.
Similarly, we found out 3:2 ratio also sounds interesting, which we later called "a fifth". And then ratios of 5:4 and 6:5, which are today known as major and minor thirds, respectively.
Sometime in the dawn of history, people noticed those intervals sounded nice without understanding all this ratios talk - it's only later that we figured out WHY they sounded like that. But as this comes from easily observable phenomena of sound, it's likely that some extraterrestrial near Proxima Centauri would notice those soundwaves fit together equally as neatly as well. He wouldn't even need an ear for that - as sound is a stream of quick changes in air pressure, he'd be able to observe the same peculiarities using some other tools.
So in a way, intervals like octaves and fifths really are universal constructs. They were discovered, not invented.
Going on, if you take some random sound from nature and find its fifth interval (by satisfying the 3:2 ratio, which means multiplying its frequency by 1.5), and then find a fifth of that frequency, and so on and so on, after 12 rounds of that you get to the seventh octave of the note you started from. And the 12 fifths you found? Those frequencies would match what today we call notes.
We actually use this system of stacking fifths in a graphic tool simply called a "circle of fifths", which uncovers even more interesting relations between the notes, like how many sharps or flats there are in a certain key:
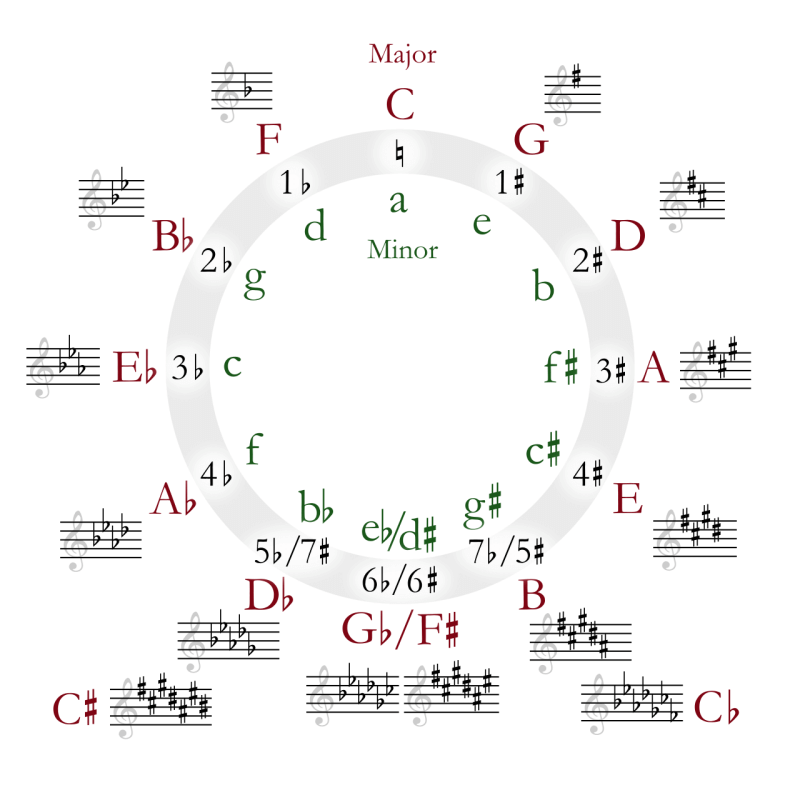
Now, is it only a mathematical coincidence that raising 1,5 to a power of 12 (finding a 12th fifth) gets you roughly the same number as 2 to the power of 7 (finding a seventh octave)? I don't know, but some alien might likely figure out the same thing and build a 12-note music system similar to our own.
Going even deeper, in the Chords Under Distortion section we mentioned the harmonic series and how each note actually has traces of all the other possible notes inside of it. Take any sound with a fixed pitch and you can find all the other pitches that will sound fine with it, and call them notes. This is crazy, it's like having an alphabet where each letter contains all the other letters inside of it. One more thing aliens could discover and end up with the music like ours.
However, this would probably be the point where we'd diverge. The evidence for this is that we already did diverge right here on our planet of Earth, as not all cultures ended up using the same musical system.
While 12-tone temperament seems global to us westerners, we know that Turkish and Arab-influenced parts of the world actually split an octave into 24 notes. We can shoehorn those additional microtones in our 12-note system by calling some of them half-flats or half-sharps, but in actuality this is a completely different system from what we're using. Different concepts, instruments and tunings, bigger focus on melody over harmony and improvisation over composition. And it's not even one system, as it varies whether you're talking about Indian, Chinese or Mongolian music. In fact, all the music theory from those two posts is about the western system, and the other system's analogues might not even match ours one-to-one.
I didn't find a simple-enough primer on the topic of those differences and the history of how they came to be, so I just have more questions about them. For example, did one of them evolve from the other? Or did they come up separately? If so, which came first?
But the point is - while extraterrestrials might end up with a 12-note system like ours, the fact that neither we did it universally makes me suspect it a bit.
One more point of contention regarding this is - what do we use as a base pitch to construct our 12 (or however many) notes from? Westerners settled on an A440 system, where the base note is middle A with a frequency of 440 Hz. But this is an arbitrarily chosen number without any significance. In history, this number varied wildly, so we settled on at least something so all our instruments are in tune with each other.
Whatever aliens chose for this value won't be 440 Hz. Firstly because hertz are tied to seconds, and it would be a gross misappropriation to think aliens tracked time in seconds, a length of time we ended up with only because Sumerians liked the number 60. So whatever aliens chose for their base frequency, in our units most likely won't be a whole number at all.
As an example of all of this, we can take a look at the aliens that we have on Earth - birds. Can we categorize bird song as music, does it follow the same rules?
Well, no. You can find videos like this one, where the bird hits a clean note C, which would imply it knows our notes and uses the same base pitch (440 Hz) as we do, but that's a crappadoodle. Find a random bird sample on Youtube and analyze what it's singing using some pitch analyzer app, and it's highly likely what you see won't match the notes we're using.
They don't appear to use the pitches in fixed steps at all. Not even 24- or 48-step, so we can't say they're microtonal. Instead of that, they do a lot of sliding motions, without settling on some concrete pitches.
The structure of their melodies does match ours, but so does human speech in general, with things like stress, intonation and natural resolve at the end of a sentence. Instead of an art form, birdsong to birds might be more akin to a communication method then, so it would be completely unfair to dunk on it for not being a "real music" based on some human-defined concepts.
It wouldn't be a stretch to say our music was inspired by birdsong though, because it sounded nice to us. But even that is not universal - it sounded nice because we've evolved in a world where birds chirping didn't threaten us. But what sounds like a pretty song to us would be a death shriek for a hapless insect on the ground.
What still remains universal are the intervals. In the video linked above, it's obvious this bird really knows its intervals, and some studies have shown that a bird's reproductive success might be related to its ability to sing as cleanest fifth interval as possible.
So with that, the birds definitely have a solid foundation to devise a full music theory framework if they reach superintelligence someday. If they were to get their stuff together, they would probably formalize what they are singing into a limited set of pitches (notes), their possible combinations (chords), and so on until they end up with a system probably really similar to ours. I'm not saying we should be scared of them. But one day, Wolfgang Amadeus Crowzart will be born, he'll write a masterpiece and you'll lose your job as a session musician. You've been warned.
Further on, all this talk assumes one thing - that music can only be made from sound. This is obvious to us, living on a planet with an atmosphere where sound can exist, and was often crucial for survival. But take for an example, an alien species living on an atmosphere-free planet revolving around a magnetar instead of a regular star. Instead of light and heat from the sun, the life there would have to appear and subsist on the magnetic fields, and the species there might evolve to be highly sensitive to the changes in magnetic fields, like we are to sounds.
Magnetic waves, while not exactly the same thing as sound waves, also come in frequencies that could be mapped to pitches (notes). A magnetic wave can also have intervals, like a fifth or an octave. You can combine multiple different waves and get a magnetic chord. And build a music theory out of it.
Same thing with electromagnetic waves, and as such, with visible light, or seismic waves. Hell, maybe even with gravitational waves, if you're big enough. Depending on which sensing organs you developed, all of those waves can be "heard" just like we hear sounds.
In fact, the way we record and play our sound-based music today is done via microphones, pickups and speakers - which are all just magnets. So basically we're already using magnet-based music, just with extra steps.
And developing specialized organs for that is not that impossible, even on Earth. Birds have a certain protein in their eyes that allows them to "see" the Earth's magnetic field, which is how they're able to navigate to warmer climates. There are also fish with organs to sense electric fields. And of course, our sense of vision is a narrow-band electromagnetic wave sensor.
To sum it up, the truth is halfway there. Whatever organs those hypothetical aliens will end up having, and whatever type of waves they will sense with them, they'll likely stumble on the same basic blocks that we did - same basic intervals, and as such notes, and as such scales and chords. But everything after that might be completely different.
Few More Random Tidbits
For the end, here's a few more interesting things.
In a 4/4 measure, the audience usually claps on beats 2 and 4. But what happens if for some reason they do it on 1 and 3? This is a problem because by clapping on 1, the audience is the one dictating the rhythm, which can throw the musician off. In this video, Harry Connick Jr. fixes the problem by sneaking in an additional beat in a song, making it 5/4 for one bar, which switches the audience's clapping from 1 & 3 to 2 & 4.
Interestingly, he wouldn't be able to do that if other members played their parts at the same time, so he had to do this before they joined.
I didn't talk much about tuning systems. But in short, historically there was a bit of a kerfuffle on the question of how exactly to split an octave into notes while preserving the clean interval ratios. Mathematically, that just doesn't work and you end up with instruments that are soft-locked to only sound good in one key. To fix this, we thought of equal temperament, which uses intervals that are slightly off from what they physically should be. For example, a fifth on a piano is not exactly 3:2, but rather something like 2.996:2. This is good enough, and it allows us to have instruments that are not locked to playing in a single key.
All modern key- and fret-based instruments work like this, so you can never really play the most correct interval on them. But on fretless instruments like violin, or with human voice, you can. If you're trying to harmonize over a note, you'll naturally gravitate towards the most correct interval, because a 3:2 fifth will resonate more than a 2.996:2 fifth. This is barely perceptible, but it's what makes choirs like barbershop quarters sound so good - the chords they are singing are using the most correct of the intervals, which you can never get on a tuned instrument like a guitar or a piano.
Their chords sound better because they're not bound by the equal temperament system, which after all was just a compromise we had to take. And it's easy to see here why - however nice barbershop quartet's just temperament system sounded, you can't really play a guitar or a piano alongside it. Which is why they themselves never do it. With equal temperament that we have today, you can do it, but at the expense of harmonies not being 100% correct. But it does sound good enough that it's for all practical terms completely imperceptible to most of us.
The End
Congrats on sticking through another 5000 words of this. If you liked it so far, I'm probably gonna do yet another one sometime in the future, so please do subscribe to my rarely-posted-on newsletter or join this sparsely-populated Discord server to stay in the loop. Cheers.